One of the things I really started wrapping my head around while I was writing math lessons at the K20 Center was the power of the narrative. As a teacher, I did not really convey a story line to my students that had much meaning at all. The chapter names of my math teaching book would have likely been Unit 1, Unit 2, and so on. Of course, the underlying concepts were there, so I’d probably have to add subtitles. Either way, there wasn’t a real story that the students could latch on to. As I thought about tasks, activities, and assessments, I didn’t filter my decisions through any real critique except whether it was easy enough to carry out, believable enough to think it would work with my kids, and if the concept was in line with the content in my book.
As I re-entered the classroom after working on lessons for some four years at the K20 Center, I was hyper-focused on narrative. In large part, I minimized the mathematical flow of my curriculum and went straight for story lines that were interesting. This meant my Algebra 1 students engaged in activities around Rate of Change for nearly the entire first month, well before my book and curriculum guide said they were ready for it. Sure, it was difficult, but our emphasis was on answering questions like Who’s faster, and How long would it take, instead of How do we do slope? The biggest change for me was thinking about how to teach a concept in a way that was situated in a context that was meaningful for the students while making the mathematics explicit.
The argument within the Math Teaching Practice #1 suggests that the “mathematical purpose of a lesson should not be a mystery to students” (p.13). The President of NCTM, Diane Briars, presented her version of this practice at the National Council of Supervisors of Mathematics (NCSM) conference this past April. She elaborated on this idea, saying the mathematics should be explicit to the learner. Deborah Ball argued that explicit should not be confused with direct. This connects well to a few of the later practices, but I do find that identifying mathematics goals that are not just goals from the textbook is incredibly challenging. Principles to Actions lays out four crucial questions that both students and teachers should be able to answer:
- What mathematics is being learned?
- Why is it important?
- How does it relate to what has already been learned?
- Where are these mathematical ideas going? (p.13)
I think that different people answer questions like these differently. I suppose the growth I made after working at the K20 Center really helped me to answer questions 2-4 much more clearly. I really had an enormous change in my approach when I started answering question 2 with more authentic answers. I suppose this is exactly what I love about the MTPs: they are kindling for awesome reflection!
One of my favorite parts of the book are the “Teacher and Student Actions” that conclude each chapter. I read these and they really hit me where it counts. I can see some areas that I nailed. Other areas, I want to skim past and ignore, partially out of the shame I have thinking about how little those things happened. Take a moment to process these actions: Are these things happening in your classroom? How often?
Establish mathematics goals to focus learning
Teacher and Student Actions
[one_half]What are teachers doing?
- Establish clear goals that articulate the mathematics that students are learning as a result of instruction in a lesson, over a series of lessons, or throughout a unit.
- Identifying how the goals fit within a mathematics learning progression.
- Discussing and referring to the mathematical purpose and goal of a lesson during instruction to ensure that students understand how the current work contributes to their learning.
- Using the mathematics goals to guide lesson planning and reflection and to make in-the-moment decisions during instruction.[/one_half]
What are students doing?
- Engaging in discussions of the mathematical purpose and goals related to their current work in the mathematics classroom (e.g., What are we learning? Why are we learning it?)
- Using the learning goals to stay focused on their progress in improving their understanding of mathematics content and proficiency in using mathematical practices.
- Connecting their current work with the mathematics that they studied previously and seeing where the mathematics is going.
- Assess and monitoring their own understanding and progress toward the mathematics learning goals.[/one_half_last]
Classroom Implications
I think there are some pretty easy ways to immediately respond to this practice. First, ask yourself what are your goals for the mathematics the students experience. How do you ensure the students are connected to those goals without reducing the instruction into a lecture that makes parts of the learning process more direct than explicit?
If you’re having trouble getting started, some wonderful OKMath Teachers took a great first stab at it. Find the elementary companion guides here, the secondary progressions here, and the secondary companion guides here.
These are only a launching point, providing something that might be completely new to some teachers and formalizing something that might be familiar to others. They have Learning Goals; “I can” and “Students will” statements; and they connect to the Priority Academic Student Skills that are back from the grave in Oklahoma. They include misconceptions and some narrative about how each relates to what happened before and what will happen next. But there is a next level out there: We can and should be thinking not only about how the individual standards are sequenced, but we should also be thinking more about how the connected standards can be leveraged.
For example, here’s the Eighth Grade Learning Goal #2 from the Secondary Progressions mentioned above:
My students will develop an understanding of inverse operations and use them to solve multi-step equations, inequalities, and basic formulas.
This goal is great. The companion guide is even better as it really provides an answer to each of the four questions above. Perhaps, though, the possibility that this Goal could leverage other standards as a context is something that deserves consideration. According to the guide, students already have some experience with two-step equations and properties of equalities, so part of this goal is about extending what is already supposedly mastered.
Here’s my take on the likely approach to this goal:
- Warm-up with one-step equations.
- Reinforce one- and two-step equations with practice examples, highlighting Properties of Equalities and useful vocabulary.
- Introduce multi-step problems – practice multiple formats
- Introduce multi-step inequalities – practice multiple formats
- Introduce formulas (one-, two-, and multi-step) – practice
- Assign class work/homework.
(Summarized from example lessons here and here.)
The opportunity to connect the concepts to prior experiences is quite narrow and does more to create a limited perspective of mathematics as a discrete set of concepts rather than an interwoven network of concepts. The utilization of some 7th grade geometry concepts can create a context by which the students can have meaningful conversations and discoveries.
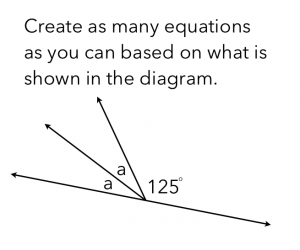
Here’s a possible warm-up that is in a familiar context, supplementary angles, and requires that the students think deeply about what information is provided, what information is assumed, and what constitutes all equations for the mathematical scenario.
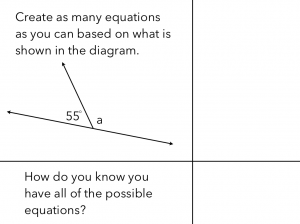
I like this question because it invokes a familiar concept for the students. We could build on other geometric examples to get to the full extent of the Learning Goal.
In each task, the interesting part is really in the challenge to create all of the possible equations. Defining a+a+125=180 as 2a+125=180 is one thing. Rewriting it as 180-125=2a and other versions is something that pushes one’s thinking about equations and the properties of equality.
There are certainly many other iterations of this Learning Goal, but the key point is that we should be restless in our pursuit of the narrative that make the mathematics resonate for our learners. Just because multi-step equations happen after one- and two-step equations doesn’t necessarily mean they should only happen in those contexts. Instead of focusing on the mathematics the students will be doing, consider the mathematics the students will be learning. This is the crux of this Math Teaching Practice and should certainly be a point of contemplation as we strive to ensure success for all students.
Reflection Questions:
- How do you ensure the mathematics you teach is connected to Learning Goals?
- What are your best and worst Learning Goals and why?
- How do you know a good Learning Goal when you see it?
- How do you ensure the mathematics is addressed explicitly, but not taught directly?
- How would you revise the example tasks to address the identified Learning Goal more accurately?
- How could you revise the Learning Goal to address the mathematical narrative more accurately?
- From the Principles to Actions Study Guide suggests the following activity: Observe or record a mathematics lesson. Use the “Teacher and student actions” chart (shown in this post) to evaluate how the lesson applies the Mathematical Teaching Practice Establish mathematics goals to focus learning. What evidence do you see of the teacher and student actions identified in the chart? Where do you see missed opportunities for these teacher and student actions? Give specific examples of evidence of this Mathematics Teaching Practice and ways to enhance the practice in future lessons.
Do you have a reflection question that others might like? Add it in the comments section below!
I hope you enjoyed this recap of the first Mathematical Teaching Practice. Remember, you can download the entire book for only $5 at NCTM’s website.