What is perseverance? The first of the Mathematics Practices from the Common Core State Standards placed this buzzword front and center in our consideration. As it turns out, it is quite easy to agree that perseverance is essential in students’ approach to mathematics. The harder question is how do we teach it.
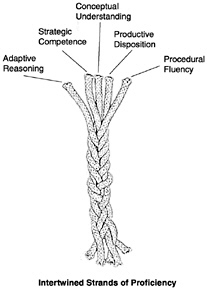
The National Research Council (NRC), in 2001, published their landmark mathematics document, “Adding It Up: Helping Children Learn Mathematics” (Read the entire book at the National Academies Press for free.) Among a host of insights provided, the essential takeaway is their identification of the Five Strands of Mathematical Proficiency (introduced on page 5), which includes “Productive Disposition.”
Mathematical Proficiency
Our analyses of the mathematics to be learned, our reading of the research in cognitive psychology and mathematics education, our experience as learners and teachers of mathematics, and our judgment as to the mathematical knowledge, understanding, and skill people need today have led us to adopt a composite, comprehensive view of successful mathematics learning. Recognizing that no term captures completely all aspects of expertise, competence, knowledge, and facility in mathematics, we have chosen mathematical proficiency to capture what we think it means for anyone to learn mathematics successfully. Mathematical proficiency, as we see it, has five strands:
conceptual understanding—comprehension of mathematical concepts, operations, and relations
procedural fluency—skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
strategic competence—ability to formulate, represent, and solve mathematical problems
adaptive reasoning—capacity for logical thought, reflection, explanation, and justification
productive disposition—habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy.
The most important observation we make about these five strands is that they are interwoven and interdependent. This observation has implications for how students acquire mathematical proficiency, how teachers develop that proficiency in their students, and how teachers are educated to achieve that goal.
Found within “productive disposition” is not the first reference to perseverance in the world of mathematics education, but one of the first to bring it to the widespread attention of mathematics teachers across the country. Here, the “belief in diligence and one’s own efficacy” is interwoven in the mathematical habits that are suggested as essential to the successful learning of mathematics.
In asking some peers through Twitter, I heard similar statements promoting perseverance:
@_levi_ too many kids just give up when things are hard. We HAVE to teach the never say die mentality! TEACH IT!
— Ann Millington-Nutt (@ann_nutt) July 16, 2014
@_levi_ practice perseverance in phases similar to building stamina. If first tasks are too complicated they give up rather than enduring.
— Julie Owens (@owens_julie) July 16, 2014
@_levi_ I feel perseverance in math is important! Too many want the answer, but sometimes you have to work and make mistakes b4 achieving — Anthony Purcell (@MrP_tchr) July 16, 2014
The interest in teaching perseverance is increasing not only because of the NRC and Common Core, but because we all know that it is essential. If not for our parents instilling it in us, we see it as an essential characteristic that is the foundation of much of the American spirit and certainly quintessential of the “Okies” who have overcome so much. While perseverance is an interest area of mine, I would not say I am an expert in teaching it. Thankfully, the topic arose at the recent OKMath EdCamp, the un-conference within Vision 2020, and I stumbled upon a few educators who have something to share on this issue. Out of the kindness of their hearts, they agreed to share some of their experiences with perseverance.
For right now, I’m only including the audio, which is available here and on the OKMath Teachers Podcast. I’ll post the video when it is ready. If you do have questions, please ask them in the comments.
[scbutton link=”http://okmathteachers.com/wp-content/uploads/2014/07/OKMath-Podcast-8.mp3″ target=”blank” variation=”steel_blue” size=”small” align=”center”]Download the Podcast[/scbutton] [scbutton link=”https://itunes.apple.com/us/podcast/okmath-teachers-okmath-podcast/id792732243?mt=2″ target=”blank” variation=”dark_grey” size=”small” align=”center”]Subscribe to the Podcast[/scbutton]
