Welcome to Week #4 of the first cycle of the Math Task Force! Glad to have you back again! Well, we needed a couple of weeks off and we think you did too. This week we’re looking forward to introducing you to the content focus that will shape the shared math tasks we introduce next week. While you can join us at this point, we recommend reading Week #1, #2, and #3 so you can catch up.
[This warm up only lasts about 10-15 minutes. If you have the endurance for it, you can also do the Heavy Lift set that should last about 15 minutes.]
Part 1) Stretch It Out
With the new Oklahoma Academic Standard for Mathematics comes new content for almost all grade levels. This new content was delicately placed in a learning trajectory across PK-Algebra 2 for students to experience mathematics conceptually, abstractly, and procedurally. As time unfolds and the school year continues, you are becoming more and more familiar with your own specific content along with how this content intertwines with and is perpetuated by the Mathematical Actions and Processes.
The OAS-M were never meant to be thought of as a check-list of “have to’s” that you teach once and are done with. These standards are meant to be bundled together, thus creating a true mathematical learning experience for students in which they interact with various mathematical concepts that are interconnected in some way, shape, or form. This idea of bundling standards is not completely new, just a unique and different way to think about the specific mathematics content you will teach at your grade level. In the real world, mathematics is not compartmentalized into isolated concepts so neither should the mathematical learning experiences of students within the classroom.
In the table below, find your specific grade level. Analyze the objectives that have been bundled together, reading closely for similarities in the intent of the standards and the expected learning experiences students should be having.
[tabgroup][tab title=”PK” id=”1″]- PK.N.2.1 Identify the number of objects, up to 10 (5), in a row or column.
- PK.N.3.1 Compare two sets of 1-5 objects using comparative language such as same, more, or fewer.
- K.N.1.3 Use ordinal numbers to represent the position of an object in a sequence up to 10. (5)
- K.GM.2.1 Use words to compare objects according to length, size, weight, position, and location.
- 1.N.1.6 Compare and order whole numbers 0100.
- 1.N.1.7 Use knowledge of number relationships to locate the position of a given number on an open number line up to 20.
- 1.N.1.8 Use objects to represent and use words to describe the relative size of numbers, such as more than, less than, and equal to.
- 2.N.1.2 Use knowledge of number relationships to locate the position of a given whole number on an open number line up to 100.
- 2.N.1.4 Find 10 more or 10 less than a given three-digit number. Find 100 more or 100 less than a given three-digit number. (a given two-digit number; finding 100 more or less will be in a later unit)
- 2.N.1.5 Recognize when to round numbers to the nearest 10 and 100.
- 2.N.1.6 Use place value to compare and order whole numbers up to 1,000 using comparative language, numbers, and symbols (e.g., 425 > 276, 73 < 107, page 351 comes after page 350, 753 is between 700 and 800).
- 3.N.1.1 Read, write, discuss, and represent whole numbers up to 100,000. Representations may include numerals, expressions with operations, words, pictures, number lines, and manipulatives.
- 3.N.1.2 Use place value to describe whole numbers between 1,000 and 100,000 in terms of ten thousands, thousands, hundreds, tens and ones, including expanded form.
- 3.N.1.4 Use place value to compare and order whole numbers up to 100,000, using comparative language, numbers, and symbols.
- 4.N.2.5 Represent tenths and hundredths with concrete models, making connections between fractions and decimals.
- 4.N.2.7 Compare and order decimals and whole numbers using place value, a number line and models such as grids and base 10 blocks.
- 5.N.2.2 Represent, read and write decimals using place value to describe decimal numbers including fractional numbers as small as thousandths and whole numbers as large as millions.
- 5.N.3.4 Find 0.1 more than a number and 0.1 less than a number. Find 0.01 more than a number and 0.01 less than a number. Find 0.001 more than a number and 0.001 less than a number.
- 5.N.2.1 Represent decimal fractions (e.g., 1/10, 1/100 ) using a variety of models (e.g., 10 by 10 grids, rational number wheel, base ten blocks, meter stick) and make connections between fractions and decimals.
- 6.A.1.1 Plot integer- and rational-valued (limited to halves and fourths) ordered pairs as coordinates in all four quadrants and recognize the reflective relationships among coordinates that differ only by their signs.
- 6.A.1.2 Represent relationships between two varying quantities involving no more than two operations with rules, graphs, and tables, translate between any two of these representations
- 7.N.1.3 Recognize and generate equivalent representations of rational numbers, including equivalent fractions.
- 7.D.2.1 Determine the theoretical probability of an event using the ratio between the size of the event and the size of the sample space; represent probabilities as percents, fractions and decimals between 0 and 1.
- 7.D.2.2 Calculate probability as a fraction of sample space or as a fraction of area. Express probabilities as percents, decimals and fractions.
- PA.D.2.1 Calculate experimental probabilities and represent them as percents, fractions and decimals between 0 and 1 inclusive. Use experimental probabilities to make predictions when actual probabilities are unknown.
- PA.D.2.2 Determine how samples are chosen (random, limited, biased) to draw and support conclusions about generalizing a sample to a population.
- PA.D.2.3 Compare and contrast dependent and independent events.
- A1.A.1.1 Use knowledge of solving equations with rational values to represent and solve mathematical and real-world problems (e.g., angle measures, geometric formulas, science, or statistics) and interpret the solutions in the original context.
- A1.A.1.2 Solve absolute value equations and interpret the solutions in the original context.
- A1.A.2.2 Represent relationships in various contexts with compound and absolute value inequalities and solve the resulting inequalities by graphing and interpreting the solutions on a number line.
- A1.A.3.1 Solve equations involving several variables for one variable in terms of the others.
- G.2D.1.1 Apply the properties of parallel and perpendicular lines, including properties of angles formed by a transversal, to solve real-world and mathematical problems and determine if two lines are parallel, using algebraic reasoning and proofs.
- G.2D.1.2 Apply the properties of angles, including corresponding, exterior, interior, vertical, complementary, and supplementary angles to solve real- world and mathematical problems using algebraic reasoning and proofs.
- G.2D.1.5 Use coordinate geometry to represent and analyze line segments and polygons, including determining lengths, midpoints, and slopes of line segments.
- A2.F.1.1 Use algebraic, interval, and set notations to specify the domain and range of functions of various types and evaluate a function at a given point in its domain.
- A2.F.2.1 Add, subtract, multiply, and divide functions using function notation and recognize domain restrictions.
- A2.F.2.2 Combine functions by composition and recognize that, the inverse function of, if and only if
- A2.F.2.3 Find and graph the inverse of a function, if it exists, in real-world and mathematical situations. Know that the domain of a function is the range of the inverse function, and the range of the function is the domain of the inverse function.
- A2.F.1.8 Graph piecewise functions with no more than three branches (including linear, quadratic, or exponential branches) and analyze the function by identifying the domain, range, intercepts, and intervals for which it is increasing, decreasing, and constant.
- A2.D.1.2 Collect data and use scatterplots to analyze patterns and describe linear, exponential or quadratic relationships between two variables. Using graphing calculators or other appropriate technology, determine regression equation and correlation
Grab yourself a piece of paper and create a Venn Diagram. Inside each of the circles write down words or short phrases that describe the specific learning expected of students from the stated objectives above. In that overlapping space in the middle of your Venn Diagram, list the connections found between the objectives listed for your specific grade level.
As you can see, bundling is an efficient way of teaching because of the correlations and similarities that can be drawn between various objectives within your grade level content.
Part 2) Cardio
The specific bundles highlighted here for each grade play a crucial part in laying the groundwork for up-and-coming bundles that follow. The progression of bundles created within each grade level lays out a thoughtful and pragmatic order of the content standards for your grade level that will allow for students to interact with the content multiple times within the year. The repeating nature of objectives within multiple bundles allows for students to see the powerful yet flexible nature of numbers and mathematics content as different objectives are bundled together.
Our focus this week is on the specific bundles highlighted here. Let’s dive back into these bundles but this time, let’s examine them for what learning experiences it creates for the students. Since these bundles lay the foundation for what is to follow, there are desired outcomes that can be identified from these bundles, ideas or concepts that are crucial for students to learn before subsequent understanding can happen.
After reading your grade-specific bundled objectives again, what does this bundle mean that a student MUST know and be able to do? Think in terms of what learning is vital that a student must walk away after this bundle is complete.
[ideabox]After contemplating the importance of your bundle and formulating ideas of what learning outcomes your students must have, jot down your ideas here.[/ideabox]Together as #OKMath Teachers, we will be generating ideas, by grade, on the essential learning of these bundled standards. Be careful to add your ideas into the document and not delete what has been added by others. Together, we can create a shared sense of the ideas or concepts that are crucial for students to learn from these bundles before subsequent understanding can happen.
Just as a strong house cannot be built upon a weak foundation, deep and solid mathematical understanding cannot happen without foundational ideas being solidified first. As a mathematics teachers, you should deeply understand the mathematical ideas that are central to the grade level you are teaching and be able to communicate these ideas in a developmentally appropriate manner to your students. The deeper you understand the content for your grade level, the more intense learning experience you can create for your students.
Part 3) Heavy Lift
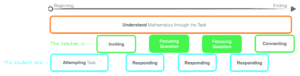
As we take a little more time to think about the specific content for your grade level, let’s revisit a visual from Week #2. (click on image to englarge)
Bundled standards fit together very nicely to allow for tasks to be effectively used within the classroom to understand mathematics deeply. A task alone cannot guarantee learning of the content by either you or your students. By utilizing efficient questioning types while teaching bundled objectives, you can create learning experiences for your students to understand mathematics deeply.
As the teacher, you must be very intentional on utilizing carefully crafted Focusing Questions to guide students through understanding the content deeply. What does it look like to ask Focusing Questions centered around your objective bundle? Let’s explore this idea a little more.
Use the graphic below to begin planning questions you can utilize next week as you implement a task centered around your specific bundled objectives. Effective focusing questions should encourage students to explain, elaborate, or clarify their thinking. Now that you know the content of these objectives deeply, what questions can you ask of your students so you can ensure they are learning the content deeply too? (click on image to englarge)
We learn best when questions come before answers. Taking time to thoughtfully prepare various types of questions ahead of time will allow for you to focus on the varied responses you could receive from your students. Successful implementation of next week’s task will center around you understanding the content deeply and the focusing questions asked of the students so they too can understand the content.
Let us know what you think here. Stayed tuned for next week’s Task Force Post because inside of it you will find your grade-specific task! These tasks will be published on Thursday, October 13 and then implemented the week of October 17.