We have been working hard for 6 weeks and the time is finally here! #OKMath Task Force is in full effect and ready to roll next week with our state-wide math tasks. Just stop for a moment and let that sink in….numerous classrooms around Oklahoma will all be doing the same task. Hundreds of students will be participating in the same engaging activity directly aligned to our new Oklahoma Academic Standards for Mathematics. How exciting!!
Part 1) Stretch It Out
Thinking back to last week, we discussed the concept of bundling, looking at our math objectives in bundled units instead of seeing them as individual ideas that are to be taught in isolation. This concept of bundled standards allows for multiple ideas to come together in a divergent way in which similarities are magnified to create real-world applications of our standards. Let’s review your grade-specific bundle of standards that your tasks will be focused upon.
[questionbox]Let’s review your grade-specific bundle of standards that your tasks will be focused upon. [/questionbox]Part 2) Cardio
For weeks now we have been working hard improving our questioning techniques and teacher moves by honing the craft in our own classroom and taking a bird’s-eye view into a fictional classroom through a crafted vignette. We all know that practice makes perfect so now is the time to put it all together in your classroom.
Below you will find your grade-specific task. Take the rest of this week to really study this task and decide when you will implement it in your classroom next week (week of October 17). Keep in mind your specific students and situation so you can make adjustments individualizing the task for you and your students. Individualizing could include technology enhancements, manipulative substitutions, or a multi-day approach based upon your class schedule.
[tabgroup][tab title=”PK Task” id=”1″]Building Block Game
http://www.prekinders.com/more-less/
Building Block Game
Children roll a game die, determine the amount represented by the numeral, and count out that many wooden cubes to stack into a tower. The die is rolled again to make a second tower. The children compare the towers to see which has the same, more, or fewer.[/tab] [tab title=”Kinder Task” id=”2″]
Button Trains
https://illuminations.nctm.org/lesson.aspx?id=276
Button Trains
Distribute to each student a bag of buttons and a 10 Strip Activity Sheet. Display a numeral less than 10, and ask the students to make a button train by putting one button into that many spaces in the 10 strip, beginning with the far left space. [This space has been bordered in a heavy line to distinguish it as the first space on the train.] When they are ready, ask the students to count the filled spaces aloud.
Then call on various students to choose a number less than 10, and ask the other students to fill that many spaces in the 10 strip. Have students count the buttons aloud to check that they have used the correct number of buttons.
Now call on a student to display his or her train and ask the other students questions such as: What button is before the red one? What button is after the green one? Which button is in the second space? Which button is between the metal button and the striped one? Request the students to pose similar questions to their peers.
Next have them place one button in each of the 10 spaces. Then call on various students to describe their button strips using ordinal language. For example, a student might say, “I put a big blue button in the first space and a little red button in the second space. Then I put a button with two holes in the third space.” As a first entry in a unit portfolio, you may wish to have the students record one way that they filled the 10 strip.[/tab] [tab title=”1st Task” id=”3″]
Comparing and Ordering Numbers (Resources Tab)
http://www.scimathmn.org/stemtc/frameworks/111b-numbers-representation-counting
Comparing and Ordering Numbers
Students need a set of number cards (5 – 35, 35-69, 70-100, or a set of thirty random numbers from 0-100). It is easy to make a number card master and reproduce on construction paper. Students cut the cards apart for a personal set.
Using number cards,
- students draw three, four, or five cards and find the number that is the greatest.
- students draw three, four or five cards and find the number that is the least.
- students draw three, four, or five cards and arrange them from least to greatest.
- students draw three, four, or five cards and arrange them from greatest to least.
Using the open number line,
- Students can place cards ranging from 1-20 on the open number when the beginning and/or end number is given.[/tab]
Open Number Line
Open Number Line
- Create pairs of number cards from index cards, one card per pair of students, ranging from 0-100. In each pair, one number should be a multiple of ten that is closest to the other number. For example, 4 & 10, 10 & 17, 20 & 29, 27 & 30, 32 & 40, 40 & 46, 50 & 58, 55 & 60, 61 & 70, 73 & 80, 80 & 86, 90 and 100.
- Give each pair of students an open number line. An open number line is an empty number line, with no numbers.
- Have each pair of students fill out the open number line in order to place their numbers in the appropriate position, labeling each interval with a whole number. (2.N.1.2)
- Allow time for the pairs of students to compare their number lines with other students’ number lines, giving them the opportunity to discover how their number lines overlap.
- In whole group, guide the students to place their number lines in order from least to greatest, overlapping as necessary
- Give each child a sticky note to record a number which is 10 more or 10 less than one of their numbers. One partner will do 10 more, and one partner will do 10 less. (2.N.1.4)
- Have them place their sticky note in the appropriate position on the number line and circle the nearest multiple of 10. (2.N.1.5)[/tab]
Number Card Activity Comparing/Ordering
Number Card Activity Comparing/Ordering
- Give students four single-digit cards. Have students organize the numbers in any way that makes sense to them. They may order their numbers from least to greatest or greatest to least (ex: 1,478 or 8,741) or organize them by odd or even (ex: 1,748) or another reason that makes sense to them. Have students share how and why they organized the digits in the way that they did.
- Once students have the opportunity to share, have them turn to their partner and look at each other’s numbers. Have students compare and contrast their two numbers, and record their findings in any way they choose. Monitor the room as they create their list, Venn diagram, etc. Have students share their findings (ex: one student has a 3 in their thousand place and the other has a one).
- With this in mind, have them consider which number is greater. Have students explain how they know. Model how to compare those numbers using symbols. Continue the task using five digit numbers as well.
Place Value Decimal Build a Number
http://www.mathwire.com/numbersense/morepv.html
Place Value Decimal Build a Number
- Select 3-6 students and give each student one of the decimal demo digit cards.
- Each student selected moves to the front of the classroom and holds the demo digit card in front of them so that classmates can easily see the numeral.
- Students at their desks should select the same digit cards from their decks and put the other cards aside.
- Give directions for students to build a number to meet specific criteria. Students in front rearrange themselves to build a number. Students at desks arrange digit cards to build a number to satisfy the conditions.
- Build the largest number you can.
- Build the smallest number you can.
- Build a number less than 70.
- Build a number greater than 400.
- Build a number that is less than 400.
- Build a number less than 4.
- Build a number that is between 40 and 70.
- Build a different number that is between 40 and 70.
- Ask students to say the number in words.
- Repeat with different digits and different directions.
- Ask students to point to the digit in the hundredths place, the tenths place, etc. Students holding cards in the front of the classroom should raise the correct card.
- Repeat this activity a few times to assess student proficiency with basic place value concepts, changing the digits and selecting different students to hold cards at the front of the classroom.
- Enrichment: As students develop proficiency with this activity, select a student to give directions for building each number to encourage the use of higher-order thinking skills.[/tab][tab title=”5th Task” id=”7″]
Decimal Fractions Match-Up
http://www.teachingideas.co.uk/subjects/fractions
http://www.teachingideas.co.uk/sites/default/files/fractionsdecimalspercentagescards_0.pdfDecimal Fractions Match-Up
Print out the decimal fractions cards and cut them apart. You will only be using the decimal, fraction, and illustration cards. Pass out cards amongst the students and then ask them to find someone else in the room that has a card that represents the exact same number. Once students think they have discovered an equivalent representation of their number, have them explain their reasoning to the entire class. Draw attention to numbers that don’t look like they are equivalent (i.e. 20/100 and .2) and ask their thoughts on why these do or do not go together.
Now have students find the equivalent to 0.1 or 0.01 more or less than their decimal. Will that change who their partner is? Once students think they have discovered an equivalent representation of their number, have them explain their reasoning to the entire class.[/tab] [tab title=”6th Task” id=”8″]
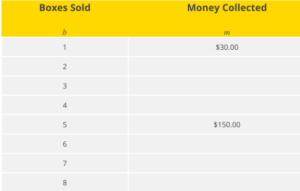
Chocolate Bar Sales
Chocolate Bar Sales
Stephanie is helping her band collect money to fund a field trip. The band decided to sell boxes of chocolate bars. Each bar sells for $1.50 and each box contains 20 bars. Below is a partial table of monies collected for different numbers of boxes sold.
- Complete the table above for values of m.
- Write an equation for the amount of money, m, that will be collected if b boxes of chocolate bars are sold. Which is the independent variable and which is the dependent variable?
- Graph the equation using the ordered pairs from the table above.
- Calculate how much money will be collected if 100 boxes of chocolate bars are sold.
- The band collected $1530.00 from chocolate bar sales. How many boxes did they sell?[/tab]
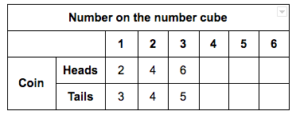
Fair Game
http://www.insidemathematics.org/assets/common-core-math-tasks/fair%20game.pdf
Fair Game
Chris and Jack are playing a board game with a fair coin and a fair number cube numbered 1 to 6.
They take turns tossing the coin and the number cube.
Then they figure out the score.
| If the coin lands on heads, the score is twice the number on the number cube.
If the coin lands on tails, the score is two more than the number on the number cube. |
Complete this table of possible scores.
1.If the score is a prime number, Chris moves two squares on the board.
If the score is not a prime number, Jack moves one square on the board.
What is the probability of getting a score that is a prime number? _____________
Show your work.
2. Chris and Jack play a game in which there are 12 trials.
How many squares would you expect Chris to move? _____________
How many squares would you expect Jack to move? _____________
3. Is this game fair? _____________
Explain your answer.[/tab] [tab title=”PreAl Task” id=”10″]
Tossing Cylinders
https://www.illustrativemathematics.org/content-standards/tasks/1047
Tossing Cylinders
Think about a cylindrical (or cylinder-like) object, such as a bottle lid or a roll of tape. Some possible objects are shown in the picture below. Suppose you were to toss one of these objects into the air and observe its landing position once it reaches the floor.
- For your object, what are the possible outcomes of this experiment?
- Make a guess – what are the probabilities of each of the possible outcomes?
- Toss the object into the air and record the outcome. Repeat this process 25 to 30 times.
- Determine the experimental probability of each outcome. How does this experimental probability compare to your guess from part b? Based on this information, would you like to change your guess?
- Repeat this activity with a different cylindrical (or cylinder-like) object that you think has a greater probability of landing on its side than your first object.[/tab]
Friends House
Friends House
This task is a little different than the other’s provided this week. It starts with a really simple introductory task that is worth doing and having conversations around, but is followed by a really nice conceptual exploration of how absolute value equations and inequalities work. This requires a little bit of a heavy-lift on your part though. You can read this very short article to get a send of the full lesson at: https://www.dropbox.com/s/advjju658c4b1j3/mt2011-04-592a.pdf?dl=0.
My friend Krista lives at 15 Sycamore Lane, and I live 8 houses away [assuming that house numbers change by units of 1]. Where could my house be located?[/tab] [tab title=”Geo Task” id=”12″]
Exploring Angle Pairs
Exploring Angle Pairs
In a DGE (Dynamic geometry Environment) construct two lines and a transversal. Have students describe the interior and exterior areas of the diagram. Measure one angle at each intersection. Have students calculate the measures for the other angles. Change the orientation of the transversal several times and have the students calculate the measures of the other angles each time. Have the students determine the relationships between certain angle pairs. Help the students name the angle pairs. Change the diagram by altering the orientation and spacing of the parallel lines. Have the students derive the rule for the measures of the angle pairs when two lines are parallel.
- Use a blank space to build the activity with students at https://www.geogebra.org/geometry.
- Use a pre-made Geogebra Explorer at https://ggbm.at/j2SVswsd (takes a few moments to load)[/tab]
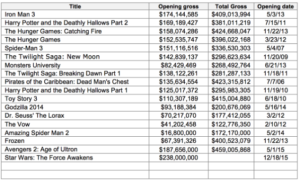
Opening Weekend
http://www.yummymath.com/wp-content/uploads/OpeningWeekendStarWars.pdf
Opening Weekend
In opening weekends, a movie’s opening gross income is often quoted as a way of measuring the movie’s eventual success. Can you predict a movie’s total gross income from its opening weekend gross income?
Here’s data on 17 movies that you might have seen (18 if you’ve already seen the new Star Wars). I’ve included the gross amount that they earned on their opening weekend (U.S.) and the gross amount that they have earned (U.S.) in total at theatres. We’ve also included the new Star Wars movie but did not give its long-term gross income.
- [/tab][/tabgroup]
Part 3) Heavy Lift
“In effective teaching, teachers use a variety of question types to assess and gather evidence of student thinking, including questions that gather information, probe understanding, make the mathematics visible, and ask students to reflect on and justify their reasoning.”
(NCTM, 2014)
Teachers have many super powers but reading the minds of our students, unfortunately, isn’t one, so we must use some of our other super powers and extraordinary skills to understand just what students are thinking when it comes to understanding math. More than ever, you are now cognizant of the types of questions you ask in your classroom to gather evidence of student thinking. As you implement your grade-specific task next week, remember to keep track of work samples. We will be doing a lot more than just grading them in the next few weeks. We will be analyzing and dissecting student answers to reflect on the lesson and student understanding.
Take a few pictures during the task. We will be sharing these pictures in our #OKMath Facebook group and the grade-specific pages. But most importantly, have fun!